CS61b:Week 7

Set&Map

我们可以用BST来构建集合或者映射。
存储集合时，一个节点只需存储集合的一个元素的值即可。
存储映射时，一个节点只需存储一对键值对即可。

B-Tree(B树)(2-3 Tree & 2-3-4 Tree)

B树（B-Tree）是一种自平衡的多路查找树。所有叶节点都处于同一层级上，确保了树的高度平衡。
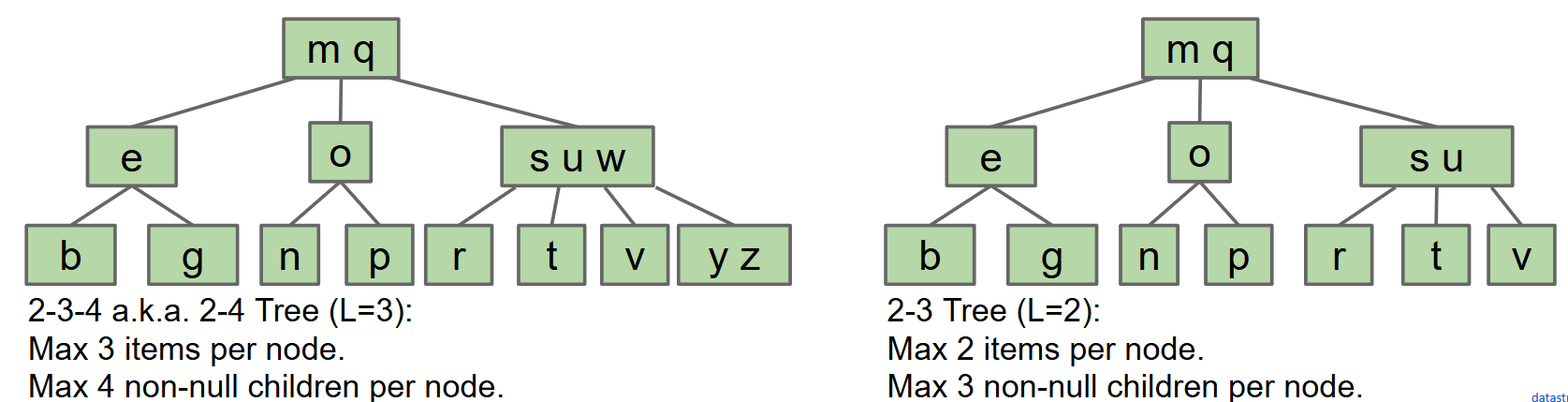
2-3树是一种特殊的B树，其中每个内部节点最多有两个或三个子节点。(每个节点的项目限制为2，即每个节点含有不超过两个项目)
2-3-4树(2-4树)，每个节点项目限制为3，每个节点可能有2，3，4个子节点。
当往二叉查找树(BST)逐渐插入越来越大的值时，不可避免地，BST的树高会逐渐增大，这使得我们遍历一棵树的所需时间变长。

B-树的构建：
- 不创建新的叶节点，把新添加的数据按序塞到已有节点中。
- 给节点的大小设置限制（如：一个节点最多包含3个元素）：如果一个节点的大小超出限制，就取出中间左边的项目，添加到父节点中
- 节点分裂：当提出节点的中间左边的值放到父节点后，该节点又以这个值为界，分割成两个子节点，左边节点的值小于提出的值，右边节点的值大于提出的值
- 但是不断增加值，直到根节点元素数量也达到限制时，按上述操作同样操作，会得到一个新的根节点，此时树高增加了一。
复杂度： $\Theta(logN)$
B树的不变量：
- 所有叶节点的节点深度都相同。（所有叶节点到根节点的距离都相同）
- 如果一个节点含有 $k$ 个项目，则其一定会有 $k+1$ 个子节点。

树旋转(Tree Rotation)

对一棵二叉搜索树进行旋转操作时，并没有改变树的任何内容，也没有改变树的语义，仅仅改变树的结构。旋转有两种方向：左旋和右旋。
将树(BST)绕一个节点进行左旋的操作是：
- 将该节点的右节点提上来作为该节点的父节点。
- 此时该节点父节点有三个子结点，提上来的节点的左节点并入该节的右节点即可。

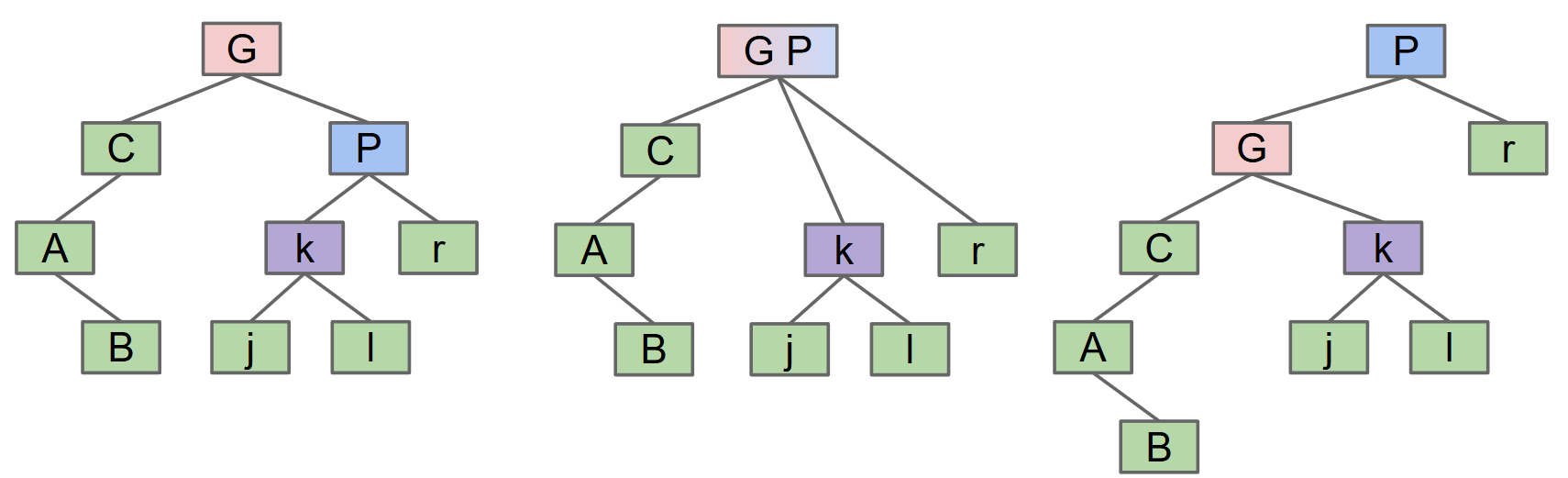
也可以看作是将该节点与其右节点暂时合并，然后将该节点向左下方分离。(带上中间的节点)!
右旋也是一样的道理，只是提上来的节点变为该节点的左节点。

平衡二叉树(AVL Trees)

平衡二叉树是一种特殊的二叉搜索树，其主要特点是任意节点的左右子树高度差不超过1。
将畸形结构的二叉树(不平衡且稀疏)通过若干次旋转将其转化成一个平衡二叉树。
时间复杂度: $O(N)$ ( $N$ 为树的大小)。对于一个大小为 $N$ 的二叉树，可以在 $N$ 步旋转内，将其转化为平衡二叉树。
2-3 tree是自平衡树。

Left Leaning Red-Black Trees(LLRBs)

左倾红黑树(LLRBs)

LLRB就是一个普通的二叉搜索树。
它保证在最坏情况下操作的复杂度为 $O(log n)$ .
使用LLRB表示B-树时，可以将B树中的一个节点中的各项目用一个虚拟链接(红线)连接起来。（并不是真正的连接，只是为了说明它们属于同一个B树中的节点）
每个2-3树都有其对应等价的LLRB，因此只要这种关系始终存在，那么LLRB就会始终保持平衡。

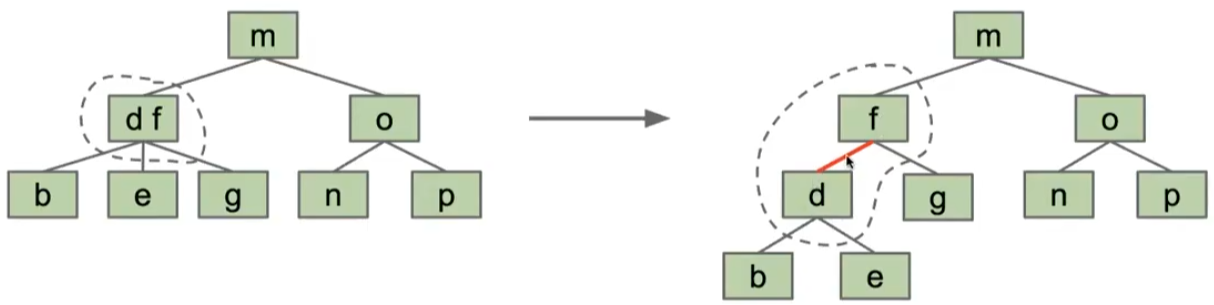
LLRB（基于2-3树）的特性：

LLRB的高度最多是其相应的B树的高度的两倍。
LLRB始终拥有对数阶渐进复杂度。
树中不存在两个连续的红色边，红色边总是向左倾斜
从根到叶子的所有路径上黑色边的数量相同，这保证了树的高度在对数级别。

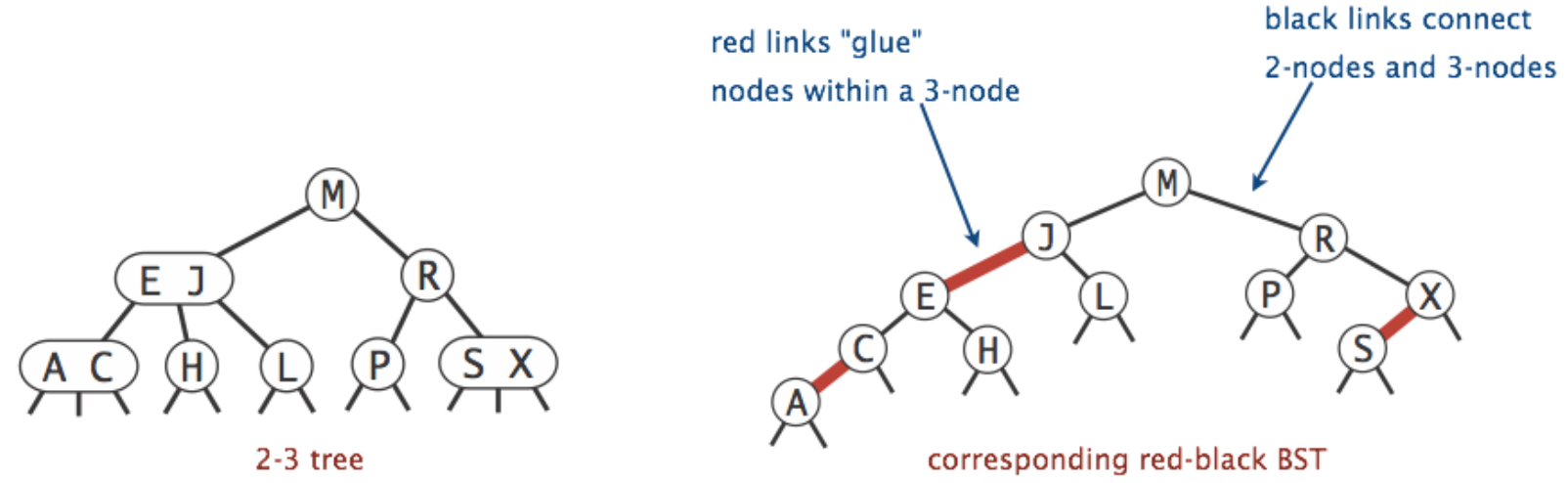
LLRB的构建(从2-3树到LLRB)：

添加新的值到红黑树时，始终新建红色的边。

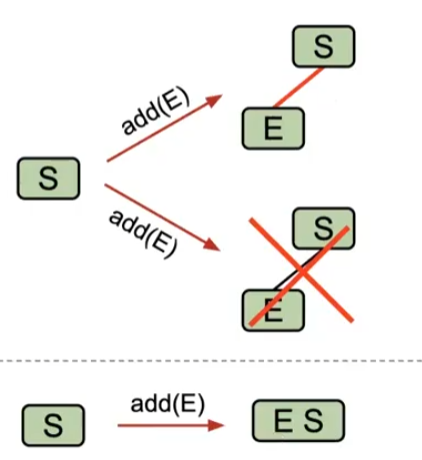
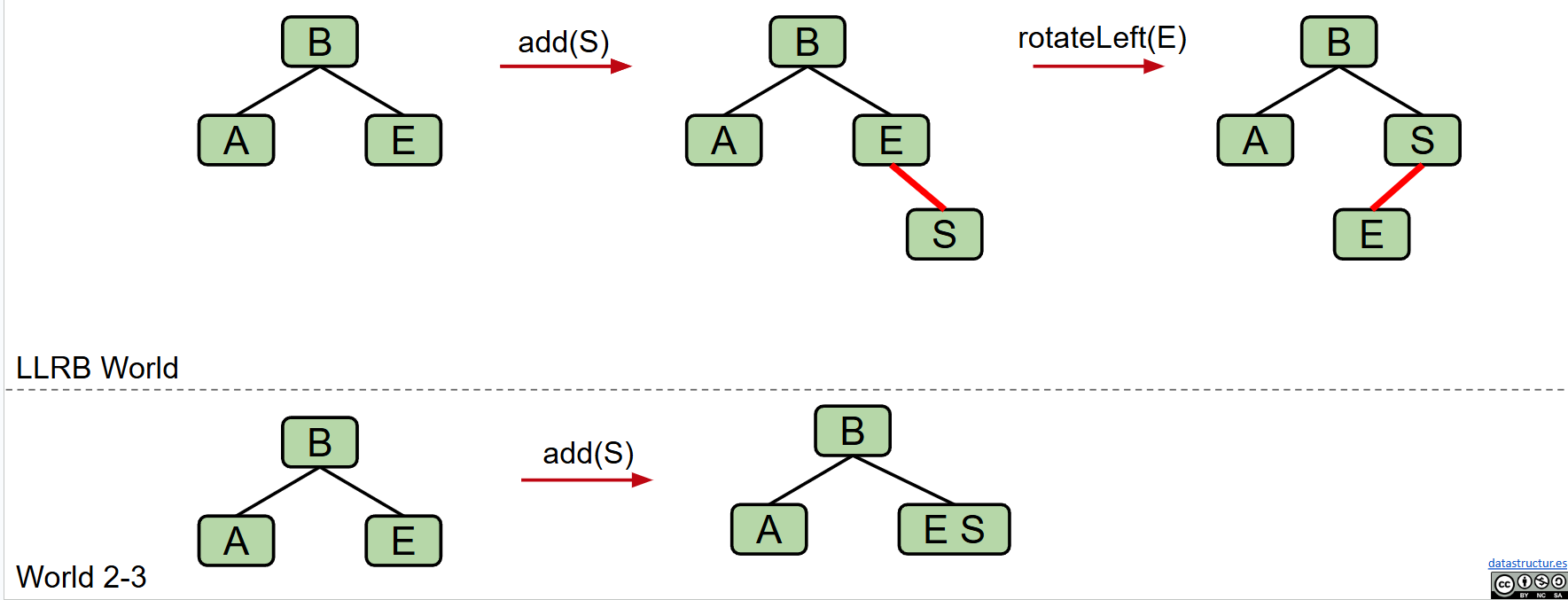
当红黑树中有向右倾斜的节点时，向左旋转修复它

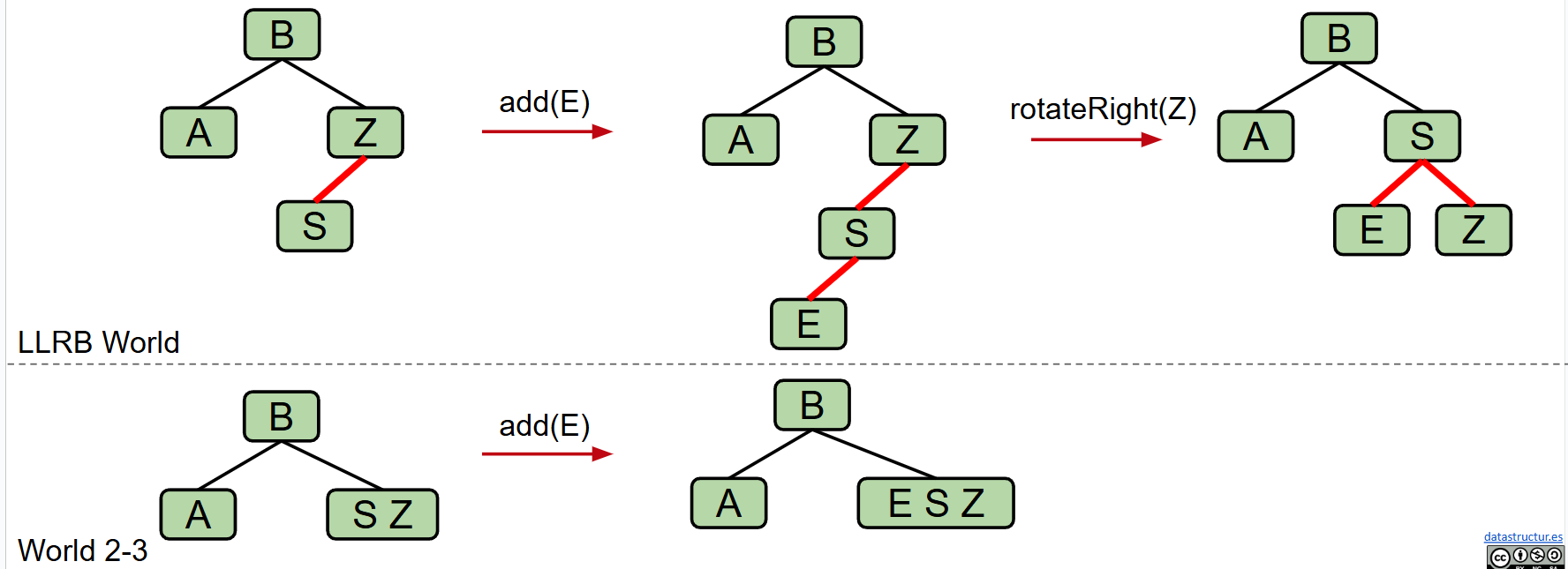
当存在两个连续的左连接时，向右旋转修复它，以获得过度填充节点(暂时状态)的正确表示。

当存在一个节点有两个红色的子节点时，反转与该节点相连的所有边的颜色。

LLRB的删除操作(EXTRA)

LLRB本质上还是属于BST的一种，故LLRB的删除操作是建立在BST删除的基础上，再对红黑树的结构加以维护。(先替代，后删除)

删除节点的分类

删除红色节点：直接删除即可
删除黑色节点：
- 该节点有一个红色节点：用红色节点代替删去的节点，并把其颜色改为黑色即可
- 该节点有两个红色节点：转化为对其子节点的删除
- 该节点为叶节点
  - 根节点直接删除
  - 删除节点的兄弟节点为黑色
    - 兄弟节点有红色子节点
      - 红色左子节点：删除结点之后，对删除节点的父节点单旋，将代替上来的节点继承原来父节点的颜色，再将其子节点染为黑色
      - 红色右子节点：删除节点之后，对删除节点的兄弟节点进行双旋，将代替上来的节点继承原来的颜色，将其子节点染为黑色
      - 左右均为红色节点：选择以上一种方法即可
    - 兄弟节点没有红色子节点
      - 父节点为红色节点
        
        删除节点后，将删除节点的父节点染黑，删除节点的兄弟节点染红。
      - 父节点为黑色节点
        
        直接把父节点当成已删除的情况处理(将父节点染黑，将其兄弟节点染红)
  - 删除节点的兄弟节点为红色(转变成黑色处理)
    - 将删除节点的父节点旋转，兄弟节点染黑，父节点染红，在使用兄弟节点为黑色的方法处理即可

Hash Table

特点：

将数据转换成哈希值。
将哈希值转化为有效的索引值。
根据得到的索引值，将数据储存在对应的桶中。
当数据的数量与桶的数量的比值超过一定限度时，扩大桶的数量以维持性能。
若保证数据的随机分布性，将会得到 $\Theta(1)$ 的平均运行时间复杂度。
不能用可变对象作为键(对象变化之后哈希值也会随之变化)
对于相同的对象，其哈希值应该相同。

使用桶来存储数据的策略

若将规模为N的数据存储在M个桶中(假设均匀分布)，理论上的时间复杂度为 $\Theta(\frac{N}{M})$
若M为常数，则相当于 $\Theta(N)$ 。只要M随着N的增大而增大，就可以实现常数复杂度(可以对 $\frac{N}{M}$ 的值设限(Load Factor)，当其超过该限制时，使M的数量加倍)
运用模运算来获取存储桶的索引(如，4400%10=0，所以存储在编号为0的桶中)，使用质数模可以获取理论上的随机性。

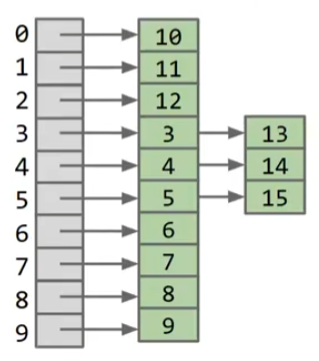
保证数据的随机分布性–均匀分布，否则会影响运行的时间复杂度,如左图数据的分布明显劣于右图

存储非整数类型的数据的策略

将数据转化为整数，在通过计算获取存储桶的索引，就可以存储到对应的桶中。
将字符串转化为整数的可能方法
- 使用字母在单词表中的位置代替字母再相加得到和。
- ASCII
- 26进制(如: $cat=3\times26^2+1\times26^1+20\times26^0=2074$ $c a t = 3 \times 2 6^{2} + 1 \times 2 6^{1} + 20 \times 2 6^{0} = 2074$
  - 这种方法使得每一个单词都存在唯一一个与其对应的数字，且具有分布的随机性。
  - 缺点：当字符集的大小十分庞大时就要使用N进制来描述（N为字符集的规模)，这使得一个字符串对应的整数可能超过JAVA中的整数所表示的范围，导致溢出。

哈希函数

将数据整数化的函数实际上叫做哈希函数，它接受一个任意类型的数据，并且返回与其对应的哈希码（整数）
哈希函数从一个无限多项的集合中取值，对应到只有有限多项的集合，因此无法为每一个字符串获取唯一与其对应的值，哈希碰撞不可避免。
哈希函数需要满足的条件
- 产生的整数最好是随机分布的整数，使得对象尽可能均匀分布在桶中。
- 对于值相等的不同对象，哈希函数要产生一个相同的哈希值。
java内置hash函数hashCode()
- java的每一个对象都拥有转化成哈希码的方法(继承自Object)，实际返回的是对象存储在内存中的地址。
java的负数取模
- 在java中，对负数进行模运算的结果仍为负数，此时不再桶列表的索引范围内，所以要使用Math类的floorMod方法，使其正确处理负数（实际上，-1%4=3）

public class ModTest {
	public static void main(String[] args) {
		System.out.println(-1 % 4);
		System.out.println(Math.floorMod(-1,4));
	}
}
//output
// -1
// 3

Hash表的检索
- 查找一个对象是否在表中时，查找函数实际上将对象转化成哈希值计算桶索引后，再在对应的桶中遍历查找对象，查找与对象值相等的项目。